Trước khi tìm hiểu chi tiết về công thức tính gốc lãi trả đều hàng tháng, chúng ta cùng điểm qua một chút về bài học cũ. Trong bài về hàm PMT trong Excel để tính số tiền thanh toán hàng kỳ cho khoản vay ta đã xác định được cách dùng hàm PMT. Nhưng để có thể phân biệt được một cách rõ ràng giữa số trả gốc và trả lãi hàng kỳ thì hãy tìm hiểu trong bài viết bên dưới nhé!
Vẫn dùng ví dụ của bài học trước để áp dụng vào trong bài học này: Bạn đang cần vay một khoản tiền là 100 triệu tại thời điểm hiện tại, yêu cầu trả liên tục hàng tháng trong vòng 3 năm với hạn mức lãi suất là 6% mỗi tháng.
Vậy là mỗi tháng bạn phải trả bao nhiêu tiền? Và tổng cộng sau 3 năm phải trả cả gốc và lãi thì sẽ là bao nhiêu tiền? Hãy cùng phân tích chi tiết số tiền gốc, tiền lãi, còn nợ của từng kỳ?
Cách làm: Để thực hiện phân tích trả nợ, ta lập 1 bảng xác định rõ từng kỳ thanh toán như bên dưới: 
- Cần xác định rõ từng kỳ thanh toán
- Tại mỗi kỳ sẽ cần xác định các chỉ tiêu: Số phải trả, Số trả gốc, Số trả lãi và số còn nợ
Mỗi chỉ tiêu sẽ được tính cụ thể như sau:
1. SỐ PHẢI TRẢ = HÀM PMT
F2 =PMT($C$4,$C$3,$C$2)
Những vị trí của tham chiếu trong hàm PMT sẽ phải được cố định để ta có thể thực hiện tính tiếp cho những kỳ sau.
Xem thêm: Hàm tìm kiếm và tính tổng trong Excel: VLOOKUP, SUM và SUMIF
2. TRẢ GỐC = HÀM PPMT (PRINCIPAL PART OF THE PAYMENT)
Cấu trúc hàm là: PPMT(Rate, Per, Nper, PV, [FV], [Type]) Tại đây sẽ xuất hiện thêm 1 tham chiếu là Per = Tại kỳ nào => Cần xác định cụ thể trả gốc vào kỳ nào. Lúc này khoản tiền này sẽ được quy đổi về giá trị tương lai của khoản tiền tại ngay thời điểm kết thúc kỳ hạn trả nợ.
G2 =PPMT($C$4,$E2,$C$3,$C$2)
3. TRẢ LÃI = HÀM IPMT (INTEREST PART OF THE PAYMENT)
Cấu trúc hàm là: IPMT(Rate, Per, Nper, PV, [FV], [Type]) Cấu trúc này sẽ tương tự như cấu trúc hàm PPMT, nhưng chỉ khác là kết quả của hàm cho bạn số tiền là số lãi phải trả, cùng với đó quy đổi về giá trị tương lai của khoản tiền tại thời điểm kết thúc kỳ hạn trả nợ.
H2 =IPMT($C$4,E2,$C$3,$C$2)
4. SỐ CÒN NỢ = KHOẢN VAY + TRẢ GỐC (VÌ TRẢ GỐC LÀ SỐ ÂM)
Số còn nợ = Khoản vay còn lại sau mỗi kỳ – Trả gốc mỗi kỳ I2 = C2+G2 I3 = I2+G3 I4=I3+G4 … => Sau đó hãy thực hiện Filldown toàn bộ công thức cho các kỳ còn lại rồi tiến hành xem kết quả: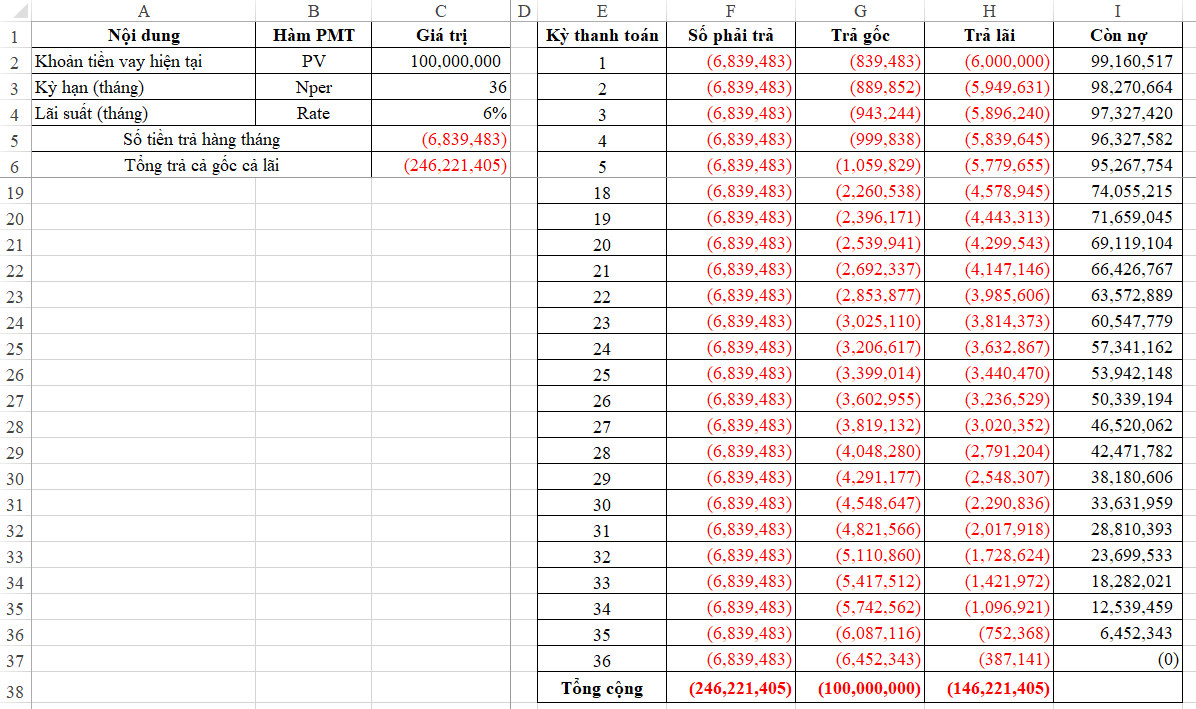 
Như vậy là ta đã có thể phân biệt được rõ ràng số gốc và số lãi trong mỗi kỳ thanh toán rồi đấy.
Tức là càng trả nhiều kỳ thì số lãi phải trả sẽ càng tăng Tiếp đến, chúng ta thử xét ví dụ trên với số kỳ trả nợ là 12 tháng xem sao nhé!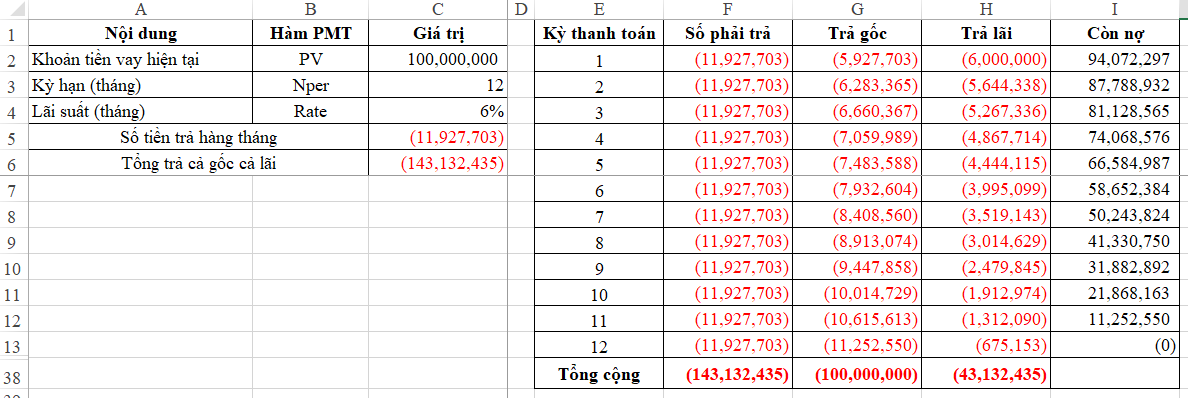 
Như vậy là chỉ cần giảm số kỳ trả lãi từ 36 xuống 12 thì ta đã giảm được hơn 100 triệu tiền lãi rồi đấy! Vậy là bạn đã học thêm được kỹ năng phân tích các khoản vay cùng với việc thanh toán vay dựa vào các hàm PMT. Đây sẽ là một kỹ năng hết sức cơ bản nhưng lại rất quan trọng mà những ai làm việc trong mảng tài chính đều cần phải nắm rõ đấy!